Implementing DES Algorithm (1977) in C
09 Sep 2018
↪ How come?
I’m generally interested in how technology inside works. A couple of month ago I started to have a closer look into the encryption algorithm AES. On youtube I found the excellent lectures from Christof Paar, held at the University of Bochum. Neither do I have a mathematical background nor do I know much about engineering so starting off with lecture #8 “Advanced Encryption Standard” was leading nowhere. I had to start from the beginning. After a couple of lessons about theoretical stuff like modulo operations and pseudo random number generators I watched Lecture #5 “Data Encryption Standard (DES)”. Since I’m a very practical person and always looking for a way to sharpen my programming skills, I thought it might be a good experience to implement my own DES library in C.
↪ Archived Publication
The original white paper dates back to July 1977, it describes the DES enciphering, the key schedule and so on. In 1999 the standard got revised and upgraded to 3DES due to several publications about successful brute force attacks within a reasonable time frame. 3DES is basically the DES algorithm applied three times on each plain text input block instead of only once.
↪ Overview
DES is a block cipher, which means that we encrypt block after block of plain text (called p) with a secret key (called k) to obtain the final enciphered text block (called e) using the function f. Key, input and output are all of the same size which is 64bit. The key schedule2 is DES’ special way to diffuse and obscure the usage of the private key, it will be described in the next paragraph in detail.
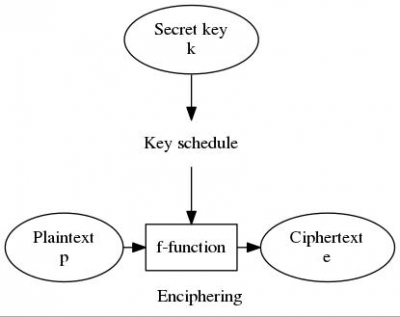
To obtain the plaint text p is to decrpyt the ciphered text e using the same DES function f and the key k, just in a reversed order of the key schedule.
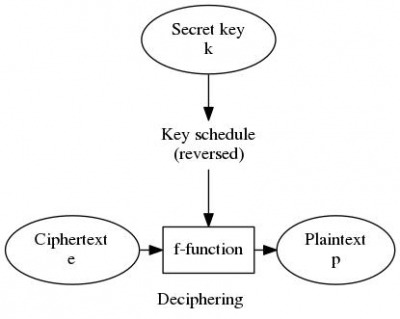
↪ Key Schedule
Here comes a tricky part: Only 56bits of the 64bit DES private key k are being used for encryption, the remaining 8bits do not increase the security but may be used for parity or something else (it is not 100% known why DES works like that) - in other words: every 8bit of the 64bit key is being thrown away.
From the original documentation, the key schedule looks like this:
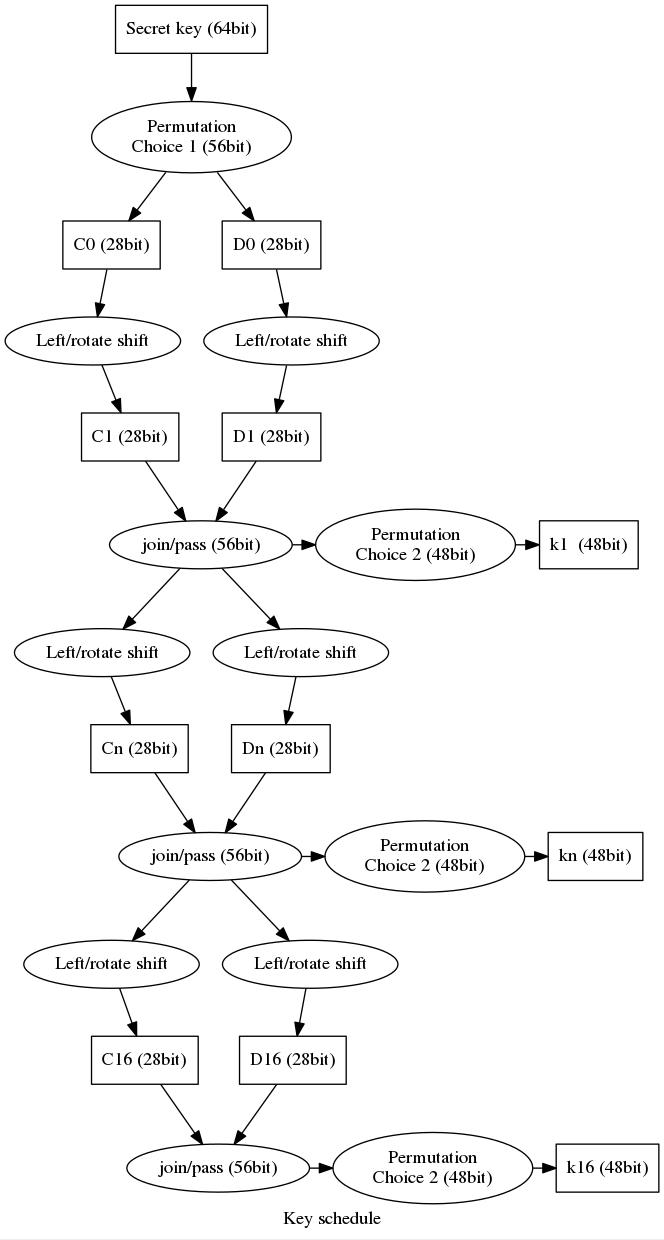
The diagram above probably looks more confusing than it actually is since we repeat the whole procedure 16 times in total. Each time the resulting key of a single step will be remembered in the key schedule as kn. At first you remove every 8th bit of the private key so it becomes 56bit. After that you use the static table Permutation choice 1 to re-arrange the order of the bits, i.e.
// Permutation choice 1
static const uint8_t PC1[PC1_LEN] = {
57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4
};
- bit 1 becomes bit 57
- bit 2 becomes bit 49
- …
- bit 55 becomes bit 12
- bit 56 becomes bit 4
The next step is to split the resulting 56bit key in half which makes c0 and d0 of 28bit size. Dependent on the current run n both subkeys have to be left-shift-rotated of p positions taken out of the Key schedule calculation table
static const uint8_t KSC[ROUNDS] = {
1, 1, 2, 2, 2, 2, 2, 2,
1, 2, 2, 2, 2, 2, 2, 1
};
Which means that in the first and second run we have to left-shift-roate each key by 1 position, from run three to 15 we have to use 2 positions, the last run will be by one position, i.e. in a 6bit world this looks like this:
- 101101 becomes 011011 in the first run
- 101101 becomes 110110 in the third run
Both rotated keys will be joined back togehter resulting in a 56bit key again, from there we have to apply table Permutation choice 2 to obtain the final 48bit key in the current run.
You have to repeat the above steps (except PC1) for 16 times to generate the final key schedule for your encryption.
↪ Enciphering computation
Once we generated all 16 keys of our key schedule we can start with enciphering our plain text. DES Enciphering computation ASCII diagram
,----------------.
| INPUT (64 bit) |
`----------------´
|
,---------------------.
| INITIAL PERMUTATION |
`---------------------´
|
L0 (32bit) <--- split ---> R0 (32 bit)
| |
| becomes L1
| ,----------. |
XOR <--- |f-function| <--- k1 |
| `----------´ |
R1-------------------------------.
| |
,------------------------------´ |
| |
L1 (32bit) R1 (32 bit)
| |
| becomes Lx
| ,----------. |
XOR <--- |f-function| <--- kx |
| `----------´ |
Rx-------------------------------.
| |
,------------------------------´ |
| |
Lx (32bit) Rx (32 bit)
| |
| becomes L16
| ,----------. |
XOR <--- |f-function| <--- k16 |
| `----------´ |
R16------------------------------.
| |
,------------------------------´ |
| |
L16 (32bit) R16 (32 bit)
| |
`--------> 64 bit joined <-------´
|
,-----------------------------.
| INVERSE INITIAL PERMUTATION |
`-----------------------------´
|
,-----------------.
| OUTPUT (64 bit) |
`-----------------´
To use all 16 keys of the key schedule we iterate over the permuted input block for 16 times, each time using a different key.
Diffuse the input of 64bit size using the Initial permutation table, again, this is quite easy:
- bit 1 becomes bit 58
- bit 2 becomes bit 50
- …
- bit 63 becomes bit 15
- bit 64 becomes bit 7 The second part of the table, called \(IP^{-1}\), is the inversed order of the Initial permutation and will be used at the last step of the DES algorithm. Just to be honest: *To me it is not clear at all what “inversed” means, I cannot see a single similarity despite the fact that both tables have numbers between 1 and 64. (Update: 2018-10-05)
// Initial and final permutation
static const uint8_t IP[2][64] = {
// IP
{
58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7
},
// IP-1
{
40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25
}
};
The permuted input will be split in two 32bit parts, l0 and r0:
l0 will be XORed with the result of the f-function (next paragraph) plus k1. The result will become r1 while r0 straight becomes l1 without any modification. The steps above will be repeated for 16 times in total.
The left part will always be XORed with the f-function plus the key, the right part will always become the left part for the next calculation.
Finally, l16 and r16 have to be rejoined to a 64bit block and \(IP^{-1}\) has to be applied. The output is the DES enciphered block of your input.
↪ The f-function
Named after the cryptographer Horst Feistel, the f-function is part of DES’ core functionality. A so called Feistel network or Feistel structure means that both encryption and decryption methods operate in an identical way, just with one important difference: the order of the key schedule. For encryption we count the key schedule from 1..16, for decryption we reverse the order from 16..1.
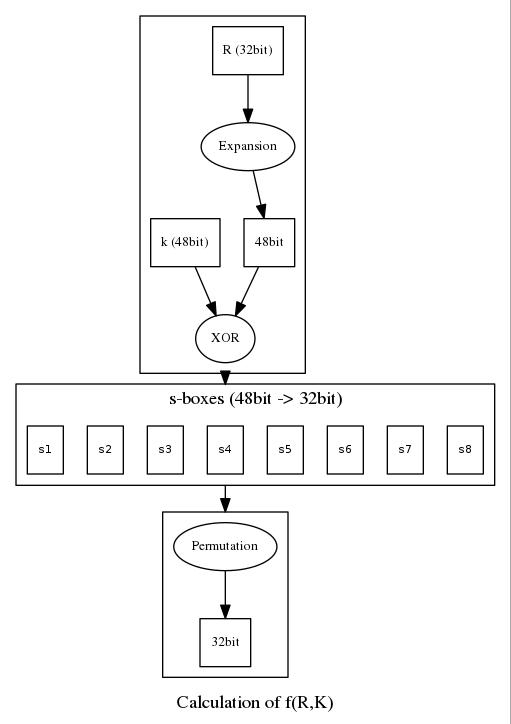
The f-function’s input is 32bit but the key has 48 bits so we have to expand the input using the Expansion permutation table:
// Expansion permutation
static const uint8_t E[EXP_LEN] = {
32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1
};
As you can see there is some redundancy in there, some bits are seen twice (1,4,5,…). These bits will be duplicated so we end up with a 48bit input block.
The expanded input will be simply XORed with the corresponding key from the key schedule in the current run.
And here comes the actual magic of the DES algorithm: The s-boxes. You can find a whole bunch of myths, conspiracies and other FUD on the internet about the s-boxes. Most of them believe that the NSA put some backdoors in them to be able to decipher your data at any time. Basically, they are fixed arrays that hold information of how to diffuse and obfuscate the bits from your input.
// The S-Boxes, 8 * 64bit
static const uint8_t S[SBOXES][SBOX_LEN] = {
// s0
{
14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13
},
// s1
{
15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9
},
// s2
{
10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12
},
// s3
{
7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14
},
// s4
{
2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3
},
// s5
{
12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13
},
// s6
{
4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12
},
// s7
{
13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11
}
};
The way how the s-boxes work is quite easy to implement, you divide 48bits by 8 and feed each s-box with one of those 6bit values. The first and the last bit of the 6 bit value in decimal representation indicate which row you have to pick, the middle 4 bits indicate the column. Return the value of the s-box that position contains and put the 8 4bit junks back together into a 32bit value.
Having an example input of 101010 as the 4th block of our 48bit input works like that:
- Get the column by using 0b101010 -> 0b10 -> 2
- Get the row by using 0b101010 -> 0b0101 -> 5
- 4th block means we have to use s3, third row, sixth column and return 11
After we computed our 32bit value we need to permute the block one last time by using the Permutation table before we return it to the Enciphering computation function.
// Permutation
static const uint8_t P[DES_LEN/2] = {
16, 7, 20, 21,
29, 12, 28, 17,
1, 15, 23, 26,
5, 18, 31, 10,
2, 8, 24, 14,
32, 27, 3, 9,
19, 13, 30, 6,
22, 11, 4, 25
};
↪ Final steps
Once finished with the steps above you just need to rejoin R16 and L16 and apply the Inversed Initial Permutation (\(IP^{-1}\), second part of the Initial Permutation array) to receive the final DES enciphered output. Yay, congratulations!
↪ Deciphering
As already said, DES is a block cipher based in the Feistel network, the enciphered text just needs to be passed through the same functions above with the reversed order of the key schedule (16..1).
↪ Source Code
The whole source code and a bit of a sample program that reads and encrypts data from STDIN with a dummy key can be found here: https://gogs.gfuzz.de/oliver.peter/DES
↪ Lessons learned
↪ Integrity and indication of success
While it might be a nice exercise to be able to encrypt a 64bit block here, in real life our data is a bit larger than that for most of the time. Just encrypting block after block and store it on your disk is not enough. You may want to have checksums, file headers and most important a way to indicate if the decryption was actually successful. The algorithm does not care about it’s content you are passing through, there has to be a way to tell your program that the plaintext which is being returned is valid.
↪ Performance
I designed my DES implementation to be more or less straight forward. As a practical person I want to understand things step by step. A quick look into some old OpenSSL commits shows that most of the things I have done in several lines could be done with a single macro and so on. To my own defense I want to mention that the OpenSSL library is more than 20 years old and maintained by more skilled mathematicians and engineers than I will ever be.
↪ Encrypting identical input blocks
If you encrypt two identical input blocks with the same key the resulting enciphered output will be the same both of the time. You may want to introduce some randomness to prohibit that behaviour i.e. add a random byte (8 bit) after every 7th input byte (56 + 8 = 64bit) to diffuse the output a bit more. That also means that you inflate the output by the factor of 1/8 size.
↪ Cryptography is hard
The things above are more about the implementation of a userland program that uses the DES cipher. The bigger problem lays in the cryptology itself. Never ever try to invent your own cryptographic cipher nor use it in production.
Use well established ciphers (like AES) instead.
↪ “Understanding Cryptography” is an excellent read
↪ Update
↪ Friday, 10th October 2018
Recently a friend of mine explained the relation between Initial Permutation \(IP\) and Inversed Initial Permutation (\(IP^{-1}\) (we count from 1 instead from 0): \(IP_{i} = j \iff IP_{j}^{-1} = i\)
- Position 1 in IP reads 58 while Position 58 in IP-1 reads 1
- Position 9 in IP reads 60 while Position 60 in IP-1 reads 9
- Position 64 in IP reads 7 while Position 7 in IP-1 reads 64
Tables: https://gogs.gfuzz.de/oliver.peter/DES/src/master/des.h