Huffman Coding (1954) - A Method for the Construction of Minimum-Redundancy
09 Sep 2018
↪ Introduction
Back in 1996 a friend at school introduced me to the MS-DOS compression program called ARJ. We used it to share some of the content of our hard disks during the break using several 3.5” floppy disks. Wikipedia states “Generally ARJ was less popular than PKZIP, but it did enjoy a niche market during the BBS era and in the warez scene” - so you might get the picture about what happened back then.
At first sight I thought that it was just a program to join multiple files into one archive and split it among several disks. However, after I extracted my first archive I was totally flushed that the resulting size of the data was more than double the size of the source. How could that be? I tried to be very clever: What happens if I compress the compressed file again? Will it shrink over and over again? Of course not. Back then, I did not know anything about compression or so called “Statistical Elimination of Redundancy”. I don’t want to claim that I know very much more about the topic today but hey, about 20 years later here comes my implementation of lossless compression.
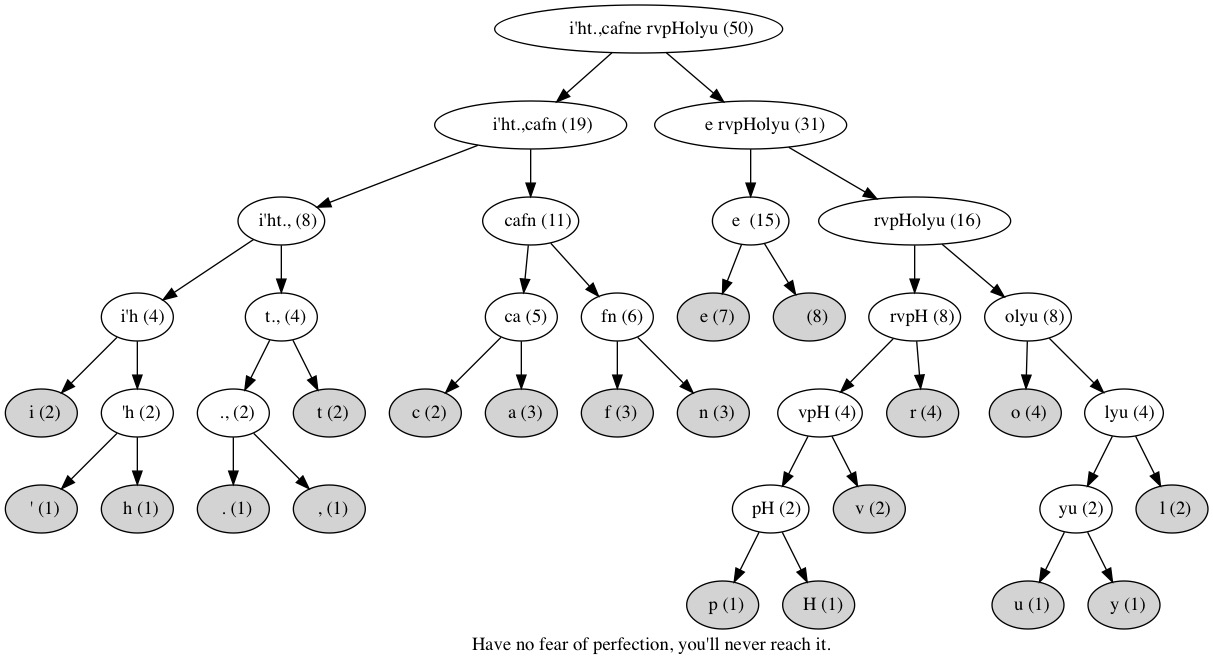
A good friend of mine recently introduced me to the Hoffman Coding, a basic concept behind compression developed by David Huffman in 1951. In our example we will use a fixed string to create the tree, the codemap and the final output.
↪ Algorithm
“Have no fear of perfection, you’ll never reach it.”
The algorithm consists of the following steps
- Count the relative frequencies of characters in our string
- Sort the list in descending order of their frequency
- Recursively join the least two frequent chars to a parent node and give it the weight of the sum of the child frequences until you end up with a single node aka the root node
- For each source character you walk from the root node left (0) or right (1) and use the resulting prefixes for the final character addressing, we only need to use the leafs, not the parent nodes.
↪ Tree and Codemap
Root i'ht.,cafne rvpHolyu
char u freq 1 code bits 6 111111
char p freq 1 code bits 6 110110
char . freq 1 code bits 5 00110
char H freq 1 code bits 6 110111
char y freq 1 code bits 6 111110
char ' freq 1 code bits 5 00010
char , freq 1 code bits 5 00111
char h freq 1 code bits 5 00011
char t freq 2 code bits 4 0010
char c freq 2 code bits 4 0100
char i freq 2 code bits 4 0000
char l freq 2 code bits 5 11110
char v freq 2 code bits 5 11010
char f freq 3 code bits 4 0110
char n freq 3 code bits 4 0111
char a freq 3 code bits 4 0101
char r freq 4 code bits 4 1100
char o freq 4 code bits 4 1110
char e freq 7 code bits 3 100
char freq 8 code bits 3 101
↪ Huffman Code
The resulting code in our example looks like this:
110111010111010100101011111101010110100010111001011110011010111
011010011000110100010000100000111001110011110111111011101111110
001011110111101010111100110101001100101110010001010100000111010
000001000110
Since we end up with binary code it is important to imagine the size of the string as length of bytes. This means that our initial string of length 50 bytes can be compressed to the size of 26 bytes. Well, the example is not 100% accurate since you would also need to include the code map into the compressed output.
↪ Source Code
The source code can be obtained here: https://gogs.gfuzz.de/oliver.peter/HuffmanCoding
↪ Lessons Learned
The example above shows that once the string has been reduced to an optimal length at a symbol level, there is now way for reduction anymore - without losing information. (Redundancy could be removed using run-length encoding by translation wwwwww to 6w but this could exceed the topic of the article…) Running compression again would also mean that we have to include another redundant code map after another; at one point the compressed output would become larger than the initial source and so on.